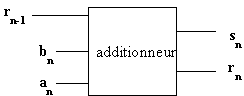
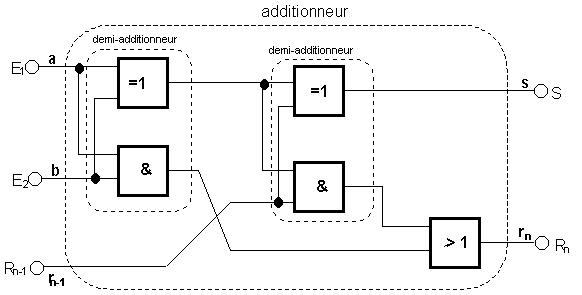
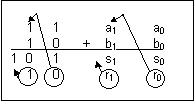
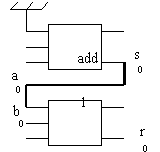
Les portes logiques

I- Objectif

Définir et étudier quelques portes logiques. Visualiser leur état binaire en sortie.

II-Présentation

Aspect technologique

Les portes logiques sont des circuits intégrés ( C.I. ) permettant de réaliser des fonctions logiques fondamentales ; ils en contiennent généralement 4 exemplaires identiques. Elles sont présentes par milliers dans les ordinateurs et permettent d'obtenir une rapidité de calcul impressionnante.

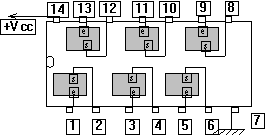
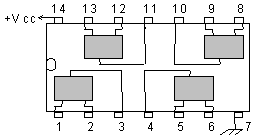
Les circuits intégrés que nous allons utiliser ont 14 broches ( 2 ´ 7 ) :

• deux sont réservées à l'alimentation ( une patte à la masse et l'autre au potentiel +Vcc ).
• les douze autres pattes concernent 4 portes identiques.

Chaque porte a, en général, deux entrées et une sortie.

Nous utiliserons des circuits de technologie CMOS (Complementary Metal Oxide Semiconductor ), mais,  il existe également des circuits de technologie TTL ( Total Transistor Logic ).

Il existe plusieurs types de portes comme nous le verrons par la suite.

Exemples de brochage :

 

 

 

 

Niveau de tension                                   

Suivant la famille logique utilisée, les tensions d'alimentation , d'entrées et de sorties varient.

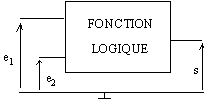
Une variable logique (dite booléenne) est une grandeur binaire: elle peut donc prendre deux valeurs  « 0 » ou « 1 ».

Sur le plan électrique, pour représenter chacune d’entre elles, il faut utiliser deux tensions.

Dans la pratique les grandeurs électriques correspondant aux grandeurs binaires sont des tensions en général continues.

Il faut dans ce cas associer à une variable logique E un signal électrique e en convenant de deux frontières e₁ et e₂.

 

Les niveaux  e₁ et e₂, très importants en pratique, dépendent de la technologie du circuit  ( TTL ou  CMOS ) et de sa tension d'alimentation V_CC. La technologie CMOS permet une meilleure tolérance en tension d’alimentation (entre 3 V et 18 V), alors que la technologie    TTL impose une tension d’alimentation de 5 V.

Par exemple avec une porte CMOS alimentée par V_CC = 9 V  : les domaines de niveau logique Bas et Haut sont obtenus à partir des tensions e₁ =2,7 V   et  e₂ = 4,9 V.

L'Algèbre de BOOLE

Une variable logique (dite booléenne) peut donc prendre deux valeurs  « 0 » ou « 1 ». Elle peut être utilisée pour représenter une proposition ou l'état d'un objet.

Exemple : elle sera égale à " 1 " pour une DEL allumée (ou tout autre dispositif), "0" si elle est éteinte.

L'algèbre de BOOLE est l'algèbre qui régit les opérations sur des variables logiques (0 ou 1)

Exemples :

L est allumée si I₁ ET I₂ sont fermés. L est allumée si I_l OU I₂ (ou les deux) sont fermés.

On peut définir deux variables logiques a et b qui représentent les états des interrupteurs I_l et I₂

a est à :            « 0 » Si I_l est ouvert,                  b est à :            « 0 » Si I₂ est ouvert.

« 1 » Si I₁ est fermé.                                         « 1 » Si I₂ est fermé.

On peut définir une fonction logique S (sortie) qui représente l'état de la lampe L :

• Si L est éteinte => S = « 0 »
• Si L est allumée =>S= « 1 »

On peut alors définir une table de vérité qui permet de connaître la valeur de la fonction logique S en fonction des diverses combinaisons des valeurs des variables a et b. Les valeurs des variables sont placées dans l'ordre binaire naturel. La table de vérité traduira le fonctionnement du système.

Exemples :

III-  LES FONCTIONS LOGIQUES DE BASE

Les fonctions logiques que nous étudierons sont :: ET, OU, NON, NON-ET, NON-OU, OU EXCLUSIF.

Pour les étudier et trouver leur tables de vérité, vous essayerez une à une les différentes portes.

                              

Etude d’une porte NON ET ( NAND ) 4011 : notion de basculement, état haut, état bas

Alimenter la platine fournie avec une tension de 5 V.

Pour visualiser l’état de sortie, plusieurs méthodes peuvent être utilisées:

VOLTMETRE                                               DEL :

 

          

                                        

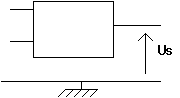
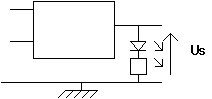
On mesure Us (Cette méthode est peu pratique) Us = 0         s = Us =    V      s =

Us = 0       : led .............................   s = Us =     V   : led .............................   s =

Pour être à l’état haut, une entrée sera mise à  e = 5 V

Pour être à l’état bas, une entrée sera mise à  e = 0 V

Remplir le tableau suivant  ( table de vérité ):

Application :

relier les deux entrées.

Etablir alors la table de vérité:                       

 

Nous avons alors réalisé un . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

 

IV- Recherche du seuil de basculement d’une porte NON

Lors de l’étude précédente, nous avons appliqué des tensions de 0 ou 5Vsur les entrées. Nous allons maintenant rechercher les domaines de tensions que l’on peut appliquer en entrée sur une porte NON pour obtenir un état haut ou un état bas

Dans ce but, la tension appliquée à l’entrée d’une porte NON étant triangulaire, nous allons étudier l’évolution de u_e et u_s en fonction du temps puis rechercher le tracé de la caractéristique de transfert de la porte u_s= f(u_e).

Matériel

-          Ordinateur + Généris

-          Multimètre numérique

-          Porte NON + Alimentation

-          GBF

Manipulation( étude à l’ordinateur)

a)       Réglages préliminaires

q       Régler le GBF à 100 Hz environ en utilisant une tension u triangulaire

q       Visualiser la tension sur Généris en mode acquisition continue après avoir fait les réglages nécessaires (visualiser deux périodes).

q       Régler la tension de sortie du GBF de façon à avoir une tension crête à crête proche de 5 V.

q       Introduire un décalage d’offset de façon que u ³0 ( la porte logique n’est pas conçue pour supporter des tensions négatives ).

b)      Réaliser le montage suivant :

                                                                                                               

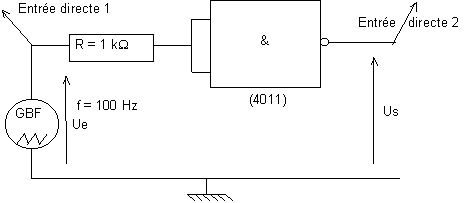c)       Enregistrement de u_e = f( t ) et u_s = f '( t ).

q       Alimenter la porte logique avec une tension de 4,9 V ( Electronic 2 ) puis réaliser le montage représenté précédemment, la tension u_e étant fournie par le GBF.

q       Réaliser le montage précédent, permettant de visualiser les tensions u_e et u_s de la porte à étudier sur les entrées analogiques Directe1 et directe 2.

q       Paramétrer le logiciel de façon à acquérir les tensions u_e sur la voie directe 1 et u_s sur la voie directe 2 pendant une durée correspondant à la visualisation de deux périodes (ou un peu plus).

q       Réaliser l’acquisition et sauvegarder dans votre répertoire sous le nom « P_LOGIC »

d)       Caractéristique de transfert

A partir des courbes précédentes, faire afficher la caractéristique de transfert u_s = f (u_e) dans une autre fenêtre. Disposer les deux fenêtres en mosaïque. Récupérer les courbes dans le compte-rendu. Imprimer.

Compte-rendu de cette partie

1)       Expliquer ce qu’est le décalage d’offset.

2)       Indiquer le paramétrage du logiciel.

3)       Interpréter la courbe représentant u_s en fonction du temps en donnant le seuil de basculement.

4)       Interpréter la caractéristique de transfert et montrer que les résultats obtenus sont en accord avec ceux du paragraphe précédent.

 

Étude des autres portes logiques

 

Utiliser la platine précédente pour tester les différentes portes fournies ( 4011 , 4070 , 4071, 4081, 4001). Pour ces portes le montage est le même car elles ont le même brochage .IL SUFFIT DE CHANGER LE C.I. APRES AVOIR éteint LE GENERATEUR.

En explorant l'ensemble des combinaisons ( E1 , E2 ) et l’état de la sortie S, nous allons établir expérimentalement le résultat de la fonction logique  S = f ( E1,E2 ) .

Consigner les résultats dans un tableau pour obtenir la table de vérité de la fonction logique considérée. 

            Rappel :

           

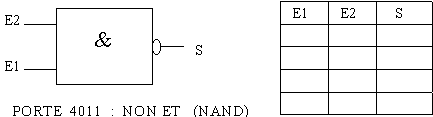
Autres portes :

 

 

 

 

 

 

 

 

 

 

 

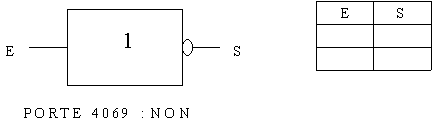
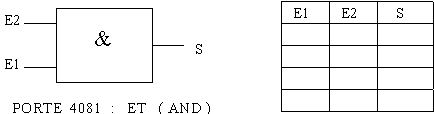
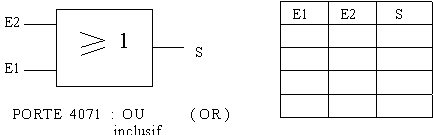
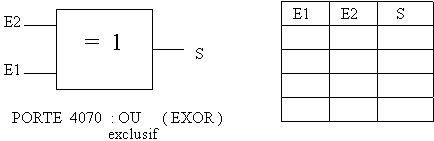
Vérifier les tables de vérité à l’aide de la simulation.

IV- Conclusion

Définir à l’aide d’une phrase conditionnelle chacune des portes précédentes.