Nous savons qu’un micro-ordinateur travaille en binaire avec des séries de 0 et de 1. Il paraît donc souhaitable de pouvoir compter aussi bien et vite que lui…
Écrire en base deux les nombres suivants en base dix: 4, 12, 25, et 67.
Écrire en base dix les nombres suivants en base deux: 1011101, 1010110101.
Essayer de faire en base deux la somme des nombres suivants:
1110 et 1011. Contrôler le résultat avec l'équivalent en base dix.
On souhaite réaliser le montage suivant (schéma n°1)proposer un schéma de branchement
avec les portes NAND.
Établir la table de vérité de ce dispositif.
Réaliser le montage et le faire vérifier.
Conclure sur l'intérêt de ce dispositif. Montrer que ce montage permet de réaliser l'addition de deux nombres binaires A et B de 1 bit chacun.
On désire maintenant additionner 2 nombres binaires de 2 bits notés A1A0 et B1B0.
Pour additionner les bits de rang 0, on utilise le montage précédent.
Pour additionner les bits de rang 1, on utilise le montage représenté sur la figure 2, la retenue éventuelle de rang 0 étant appliquée en R0.
1°) Montrer que si cette retenue est nulle (R0 = 0) le demi-additionneur 2 n'intervient pas et que la somme des bits de rang 1 apparaît en S1 et R1.
2°) On suppose ensuite que R0 = 1.
a) Établir la table de vérité du circuit du schéma 2.
b) Vérifier théoriquement que le montage global fait bien la somme des nombres binaires A1A0 et B1B0 .
3°) Vérifier expérimentalement que le montage se comporte bien comme prévu. On vérifiera les deux parties précédentes.
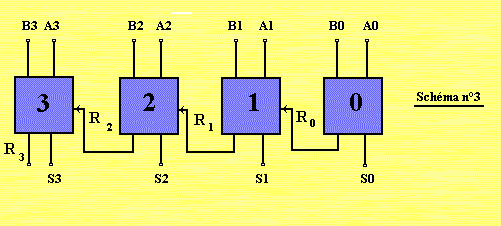
4°) Quel serait le détail d'un additionneur 4 bits dont le principe est donné au schéma 3?
5°) Associer avec un groupe voisin pour réaliser expérimentalement un additionneur 4 bits.
6°) Utiliser un additionneur du commerce (série TTL 7483) et vérifier qu’il effectue bien l’addition de deux nombres de 4 bits chacun. Dans les livres de composants les sorties sont souvent notées S 1, S 2,… et les retenues C0, …
![]()