|
Phys. N° 02 |
Les ondes périodiques progressives : Exercices |
À l’aide d’un microphone, on visualise sur la voie A d’un oscilloscope le son émis par un instrument de musique. On obtient la courbe ci-dessous.
|
|
Les réglages de l’oscilloscope sont :
- Sensibilité de la voie A : 100 mV / div ;
- Sensibilité de la voie B : 100 mV / div ;
- Balayage : 0,5 ms / div.
Déterminer la période et la longueur d’onde sachant que la célérité du son est 340 m / s.
-
Réponses :
-
Période du son : sur l’oscillogramme, la durée de deux périodes
correspond à 9 div.
-

-
Longueur d’onde du son :
-
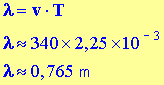
Une corde soumise à un vibreur est photographiée à l’instant t = 0,060 s, le vibreur ayant commencé à fonctionner à l’instant t = 0 s. La célérité des ondes de long de la corde est 2,0 m / s.
|
|
1)- Calculer la fréquence n et la longueur d’onde l de l’onde.
-
D’après l’enregistrement, le signal a parcouru la distance d
= 3 l pendant la durée Dt
= 0,060 s.
-
Fréquence du signal :
-

-
Longueur d’onde du signal :
-
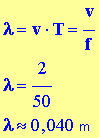
2)- Au début du fonctionnement, le vibreur s’est-il déplacé vers le bas ou vers le haut ?
- Au début du mouvement, le vibreur s’est déplacé vers le bas.
Dans une cuve à ondes, on néglige l’amortissement et la réflexion. On reproduit ci-dessous les photographies obtenues à la surface de l’eau avec différentes fréquences du vibreur. Sur la figure, 1 cm représente 4 cm.
|
|
1)- Donner la relation permettant de calculer la célérité de l’onde pour chaque valeur de la fréquence de vibration.
-
Relation permettant de calculer la célérité de l’onde :
-

2)- Déterminer dans chaque cas la valeur de la longueur d’onde.
- Valeur de la longueur d’onde pour chaque cas :
|
Fréquence |
Nombre
de longueur d’onde |
Distance
sur le schéma |
Distance réelle |
Longueur
d’onde |
|
f
1 = 20 Hz |
6
l 1 |
3
cm |
12
cm |
l 1
= 2,0 cm |
|
f
2 = 23 Hz |
7
l 2 |
3
cm |
12
cm |
l 2
= 1,7 cm |
|
f
3 = 27 Hz |
5
l 3 |
2
cm |
8
cm |
l 3
= 1,6 cm |
|
f
4 = 30 Hz |
8
l 4 |
3
cm |
12
cm |
l 4
= 1,5 cm |
3)- Calculer la célérité pour chaque valeur de la fréquence. Conclure sur le milieu de propagation.
-
Célérité de l’onde pour chaque fréquence :

|
Fréquence |
Longueur
d’onde |
Vitesse
m / s |
|
f 1
=20 Hz |
l
1 = 2,0 cm |
v 1
= 0,40 |
|
f 2
=23 Hz |
l
2 = 1,7 cm |
v 2
= 0,39 |
|
f 3
=27 Hz |
l
3 = 1,6 cm |
v 3
= 0,43 |
|
f 4
=30 Hz |
l
4 = 1,5 cm |
v 4
= 0,45 |
- La célérité de l’onde dépend de la fréquence. Le milieu est dispersif.
IV-
Exercice 26 page 65. Célérité du son.![]()
Un haut-parleur est mis en vibration à l’aide d’un G.B.F réglé sur la fréquence f = 1,47 kHz. Un microphone placé à une distance d du haut-parleur est relié à la voie B de l’oscilloscope. La voie A étant reliée au G.B.F.
- Schéma :
|
|
- On observe l’écran ci-dessous.
|
|
1)- Déterminer la durée de balayage de l’oscilloscope.
-
Durée de balayage : une période T
correspond à x ≈
7 div.
-
Période du son :

- Durée de balayage :
-

2)- Décalage q (en s) entre les deux courbes. Exprimer le temps mis par l’onde sonore pour atteindre le microphone en fonction de q, f et un nombre entier n.
-
q ≈
0,1 x 1,5
Þ
q ≈
0,15
ms
-
Temps mis par l’onde pour atteindre le micro. Le temps est connu à
un nombre entier de période T.
-
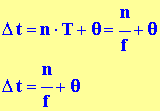
3)- Les deux voies ont la même sensibilité : k = 100 mV / div. Calculer les amplitudes des deux ondes. Pourquoi sont-elles différentes ?
- Amplitudes des deux ondes.
-
![]()
-
![]()
4)- On augmente progressivement la distance entre le microphone et le haut-parleur. Pour deux positions successives repérées par d 1 et d 2 telles que d 2 – d 1 = 23,0 cm, on obtient deux courbes en phase. En déduire la longueur d’onde l et la célérité v du son.
-
Longueur d’onde du son : l = d
2
– d
1
= 23,0 cm.
-
Célérité du son :
-

5)- Sachant que d est comprise entre 40 et 60 cm, donner sa valeur.
-

|
n |
1 |
2 |
3 |
|
d cm |
28,1 |
51,1 |
74,1 |
- Comme d est compris entre 40 et 60 cm, la bonne valeur est : d = 51,1 cm.
6)- Si on change la fréquence du G.B.F, la célérité v du son change-t-elle ? Pourquoi ?
-
La célérité du son ne change pas car l’air n’est pas un milieu
dispersif pour les sons.
À l’aide de deux microphones reliés à un oscilloscope, on visualise le son émis par un haut-parleur en deux endroits différents. Un des deux microphones est fixe, l’autre est mobile. La célérité du son est 340 m / s.
Lorsque la distance entre les deux microphones est d 1 = 51,0 cm, on observe le premier écran ci-dessous ; lorsque la distance entre les deux microphones est d 2 = 93,5 cm, on observe le second écran reproduit.


1)- Faire le schéma du montage. Justifier la différence d’amplitude sur les sinusoïdes observées.

-
Au cours de la propagation, l’onde sonore perd de l’énergie.
L’amplitude de l’onde diminue.
2)- Calculer la valeur du
rapport
![]() . Montrer que ce rapport est égal au rapport d’un nombre entier impair par
un nombre entier pair.
. Montrer que ce rapport est égal au rapport d’un nombre entier impair par
un nombre entier pair.
-
Valeur du rapport
![]() :
:
-

- Pour la distance d 1 entre les deux microphones, les deux courbes sont en phase. La distance d 1 est égale à un nombre entier de fois la longueur d’onde.
-
![]()
-
Pour la distance d 2
entre les deux microphones, les deux courbes sont en opposition de phase. La
distance d
2
est égale à un nombre entier de fois la longueur d’onde plus la moitié
d’une longueur d’onde :
-

-

3)- Donner la valeur de ces deux nombres entiers. En déduire la longueur d’onde l.
-
Recherche de k’ et k :
-

-
Longueur d’onde du son :
-

4)- Calculer la fréquence du son émis, ainsi que la vitesse de balayage de l’oscilloscope.
- Fréquence du son émis.
-

-
Durée de balayage : une période T
correspond à x = 5 div.
-
Période du son :
-

-
Durée de balayage :
-

-

5)- On place à nouveau les deux microphones 51,0 cm l’un de l’autre et on supprime le balayage (mode XY). Quelle est la forme de la courbe obtenue sur l’écran ?
-
Les deux courbes étant en phase, on visualise un segment de droite sur l’écran.
6)- On place devant le haut-parleur un obstacle comprenant une fente de 5 cm de largeur. Quel phénomène observe-t-on ?
- La largeur de la fente étant du même ordre de grandeur que la longueur d’onde du son, l’onde donne un phénomène de diffraction.