Numérotation binaire (rappel) :
Compléter le tableau ci-dessous :
| Base 10 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| Base 2 | 0 | 1 | 10 |
Exemples d’additions binaires :
| Retenue | |||||
| 0 | 0 | 1 | 11 | 101 | A |
| + 0 | + 1 | + 1 | + 10 | + 011 | B |
| Somme |
L’addition de 2 chiffres binaires peut-elle être réalisée par l’opération somme logique ?
Justifier à travers un exemple .
Écrire une table de vérité qui tienne compte des problèmes liés à l’addition binaire :
Principe :
Un demi-additionneur permet de réaliser l’addition de deux chiffres binaires E1 et E2 et affiche le résultat de l’addition sous forme d ‘une variable S et éventuellement une retenue R .

Table de vérité du demi-additionneur :
E1 |
E2 |
S |
R |
Combien d’entrées et de sorties compte le montage demi-additionneur ?
Schéma fonctionnel du demi-additionneur:
Quelles sont les fonctions logiques réalisées par le montage demi-additionneur ?
S =
R =
En déduire son schéma fonctionnel , le réaliser avec le logiciel Crocodile Clip (Logiciel de simulation de circuit électronique de la Société Pierron).
Pour additionner deux nombres binaires à plusieurs bits, il faut tenir compte de l’éventuelle retenue de l’étage précédent . Un demi-additionneur ne peut donc réaliser une telle opération. Pour éliminer cette difficulté, il faut un circuit à trois entrées : C’est l’additionneur complet:
Principe:
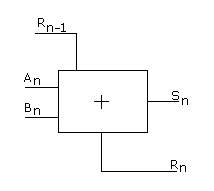
Un additionneur permet de réaliser l’addition de deux chiffres binaires E1 et E2 tout en tenant compte de la retenue Rn-1 et affiche le résultat de l’addition sous forme d ‘une variable S et éventuellement une retenue Rn.
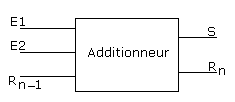

Simuler le montage ci-dessous:
Écrire la Table de vérité :
E1 |
E2 |
Rn-1 |
S |
Rn |
On veut réaliser un montage pour effectuer l’addition 101 + 011. Combien d’additionneurs contiendra ce montage ?
Simuler le montage, en réalisant d'abord le schéma fonctionnel on simplifiant un additionneur par, puis à l'aide du logiciel Crocodile Clip: